찰스 슈왑 (NYSE :SCHW)의 다가오는 미화 0.27 달러 배당금에 대해 좋아할 것이 많습니다.

일부 투자자는 자산 증식을 위해 배당금에 의존하는데, 배당금에 관심이 많은 투자자라면 찰스 슈왑 코퍼레이션(NYSE:SCHW)이 단 4일 만에 배당금을 지급할 예정이라는 사실에 흥미를 느낄 수 있을 것입니다. 배당금 지급일은 일반적으로 배당금을 받기 위해 회사 장부에 주주로 등재되어 있어야 하는 마감일인 기록일 1영업일 전으로 설정됩니다. 주식에 대한 모든 거래는 기록일 또는 그 이전에 결제되어야 하므로 배당금 지급 기산일을 알아두는 것이 중요합니다. 따라서 5월 9일 이후에 주식을 매수한 찰스 슈왑 투자자는 5월 23일에 지급되는 배당금을 받지 못합니다.

예정된 배당금은 주당 0.27달러로, 지난 12개월 동안 주주들에게 주당 총 1.08달러를 배당했던 지난 배당금에 이은 것입니다. 지난 1년간의 배당금을 계산하면 현재 주가인 83.11달러에 대해 찰스 슈왑의 후행 수익률은 1.3%입니다. 배당을 위해 이 기업을 매수한다면 Charles Schwab의 배당금이 신뢰할 수 있고 지속 가능한지 파악해야 합니다. 그렇기 때문에 배당금이 지속 가능한지, 회사가 성장하고 있는지 항상 확인해야 합니다.

AI가 의료 서비스를 바꾸고 있습니다. 이 20개 종목은 조기 진단부터 신약 개발까지 모든 분야에서 노력하고 있습니다. 가장 좋은 점은 모두 시가총액이 100억 달러 미만이라는 점이며, 아직 일찍 투자할 수 있는 시간이 있다는 것입니다.

배당금은 일반적으로 회사 이익에서 지급되므로 회사가 벌어들인 것보다 더 많은 배당금을 지급하면 일반적으로 배당금이 삭감될 위험이 더 커집니다. 찰스 슈왑은 작년에 수익의 31%를 배당금으로 지급했습니다.

회사가 수익보다 배당금을 적게 지급하면 일반적으로 배당금이 적정하다는 것을 의미합니다. 이익의 배당금 비율이 낮을수록 경기가 침체기에 접어들 때 배당금에 대한 안전 마진이 커집니다.

찰스 슈왑에 대한 최신 분석을 확인하세요.

여기를 클릭하여 회사의 배당금 비율과 향후 배당금에 대한 애널리스트 추정치를 확인하세요.

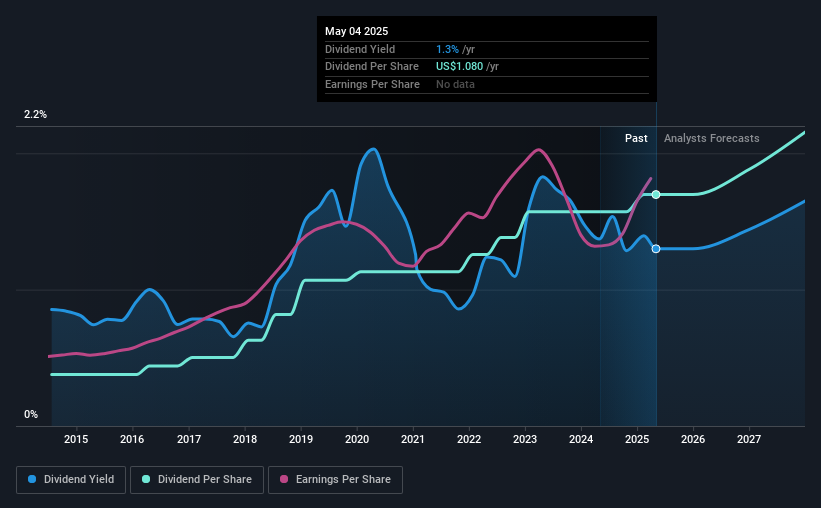
수익과 배당금이 증가하고 있습니까?

지속 가능한 수익 성장을 창출하는 기업의 주식은 수익이 상승할 때 배당금을 올리기가 더 쉽기 때문에 배당 전망이 가장 좋은 경우가 많습니다. 수익이 크게 떨어지면 회사는 배당금을 삭감해야 할 수도 있습니다. 그렇기 때문에 찰스 슈왑의 주당 순이익이 지난 5년간 연평균 4.3% 증가한 것은 다행스러운 일입니다.

대부분의 투자자가 회사의 배당 전망을 평가하는 주된 방법은 과거 배당금 증가율을 확인하는 것입니다. 찰스 슈왑은 지난 10년간 연평균 16%의 배당금 성장률을 기록했습니다. 수년에 걸쳐 수익과 함께 배당금이 증가하는 것은 회사가 주주들과 성장을 공유하려는 의지가 있다는 신호일 수 있습니다.

요약하자면

찰스 슈왑은 매력적인 배당주인가요, 아니면 그냥 두는 것이 좋을까요? 찰스 슈왑은 최근 몇 년 동안 주당 순이익이 천천히 성장하고 있으며 수익의 절반 이상을 비즈니스에 재투자하고 있어 일반적으로 미래 전망에 좋은 징조입니다. 저희는 이 조합이 매우 매력적이라고 생각하며 Charles Schwab에 대해 더 자세히 조사해보고 싶습니다.

배당금만 보고 찰스 슈왑에 투자하고 싶은 유혹이 있지만, 항상 관련된 위험을 염두에 두어야 합니다. 실례로 찰스 슈왑에서 주의해야 할 경고 신호를 1건 발견했습니다.

높은 배당금을 지급하는 종목을 찾고 계신다면, 저희가 선정한 상위 배당주를 확인해 보시기 바랍니다.

이 기사에 대한 의견이 있으신가요? 내용에 대해 궁금한 점이 있으신가요? 직접 문의해 주세요. 또는 편집팀 (at) simplywallst.com으로 이메일을 보내주세요.

이 기사는 Simply Wall St에서 작성한 일반적 성격의 글입니다. 편향되지 않은 방법론을 사용하여 과거 데이터와 애널리스트의 예측에 기반한 논평을 제공하며, 재정적 조언을 목적으로 하지 않습니다. 또한 주식 매수 또는 매도를 추천하지 않으며, 사용자의 목표나 재무 상황을 고려하지 않습니다. 저희는 펀더멘털 데이터에 기반한 장기적 관점의 분석을 제공하는 것을 목표로 합니다. 당사의 분석에는 가격에 민감한 최신 기업 발표나 정성적 자료가 고려되지 않을 수 있습니다. Simply Wall St는 언급된 주식에 대해 어떠한 포지션도 갖고 있지 않습니다.